e (რიცხვი)

ფუნქციის f(x)=e^x წარმოებულის მნიშვნელობა (მხების დახრა) წერტილში x=0 1-ის ტოლია. ნახატზე f(x)=e^x ლურჯადაა გამოსახული. შესადარებლად ნაჩვენებია ფუნქციების 2^x (წერტილოვანი) და 4^x (წყვეტილი) გრაფიკები. ამ უკანასკნელი ორი ფუნქციის წარმოებულის მნიშვნელობა წერტილში x=0 არ უდრის 1-ს.

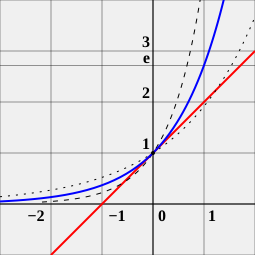
მათემატიკური მუდმივა e — ერთადერთი ნამდვილი რიცხვი, რომელიც აკმაყოფილებს შემდეგ პირობას: ფუნქციის f(x)=a^x წარმოებულის მნიშვნელობა (მხების დახრა) წერტილში x=0 არის 1 მხოლოდ და მხოლოდ მაშინ, როდესაც a=e. ფუნქციას f(x)=e^x მაჩვენებლიანი ფუნქცია ეწოდება. მისი შექცეული ფუნქციაა ნატურალური ლოგარითმი, ანუ ლოგარითმი ფუძით e. რიცხვი e-ს მრავალი განსაზღვრება არსებობს: როგორც ნატურალური ლოგარითმის ფუძე (სადაც თავად ნატურალური ლოგარითმი ინტეგრალის მეშვეობითაა განსაზღვრული); როგორც გარკვეული მიმდევრობის ზღვარი; როგორც გარკვეული მწკრივის ჯამი და სხვ.

რიცხვ e-ს ხანდახან ეილერის რიცხვი ან ნეპერის რიცხვი ეწოდება.

e, ისევე როგორც 0, 1, π და i, მათემატიკაში ერთ-ერთი უმნიშვნელოვანესი რიცხვია. ხუთივე მათგანი ეილერის იგივეობაში გვხვდება.

e ირაციონალური რიცხვია, ანუ ის ვერ ჩაიწერება მთელი რიცხვების შეფარდების სახით (იხილეთ ირაციონალურობის დამტკიცება). გარდა ამისა, e ტრანსცენდენტურია, ანუ არ არსებობს არანულოვანი მრავალწევრი რაციონალური კოეფიციენტებით, რომლის ფესვია e. e-ს ათობითი ჩანაწერია

$e=2.71828~18284~59045~23536\ldots .\!$

ისტორია

მუდმივაზე პირველი მინიშნება ჯონ ნეპერის ნაშრომში ლოგარითმების შესახებ გამოჩნდა. თუმცა თავად ნაშრომში მუდმივა არ იყო მოცემული და ის მხოლოდ ამ რიცხვის მეშვეობით გამოთვლილი ნატურალური ლოგარითმების ცხრილს შეიცავდა. მიიჩნევია, რომ ცხრილი უილიამ ოტრედმა შეადგინა. მუდმივის აღმოჩენა იაკობ ბერნულის მიეწერება, რომელმაც შემდეგი გამოსახულების მნიშვნელობის (რომელიც მართლაც e-ს ტოლია) გამოთვლა სცადა:

$\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

ეს მუდმივა (რომელიც b-თი აღინიშნებოდა) პირველად გოტფრიდ ლაიბნიცმა და კრისტიან ჰუიგენსმა გამოიყენეს თავიანთი 1690-1691 წლების მიმოწერაში. ლეონარდ ეილერმა მუდმივის აღსანიშნად ასო e-ს გამოყენება 1727 ან 1728 წელს დაიწყო. პირველი გამოცემა, რომელიც e-თი აღნიშნულ ამ მუდმივას შეიცავდა, ეილერის „მექანიკა“ (1976) იყო. მომავალში მუდმივის აღსანიშნად აგრეთვე გამოიყენებოდა ასო c, თუმცა საბოლოოდ ასო e დამკვიდრდა.

e-ს ირაციონალურობა ეილერმა 1737 წელს დაამტკიცა: მან აჩვენა, რომ e-ს უსასრულო მარტივი უწყვეტი წილადის სახე აქვს. 1844 წელს ლიუვილმა აჩვენა, რომ e არ აკმაყოფილებს არც ერთ კვადრატულ განტოლებას მთელი კოეფიციენტებით (ე.ი. დაამტკიცა, რომ თუ e ალგებრულია, მაშინ ის მეორე ხარისხზე მაღალი უნდა იყოს).

e-ს გამოყენება

რთული პროცენტის ამოცანა

იაკობ ბერნულიმ ამ მუდმივის არსებობა რთული პროცენტის დარიცხვის წესის შესწავლისას დაადგინა.

მაგალითად, დავუშვათ, მოცემულ საბანკო ანგარიშზე 1.00 ლარია. ბანკი ყოველწლიურად ჯამში 100%-ს რიცხავს. თუ დარიცხვა მხოლოდ ერთჯერადია, წლის ბოლოს ანგარიშზე 2.00 ლარი იქნება; მაგრამ თუ წელიწადში ერთხელ 100%-ის ნაცვლად ბანკი ორჯერ დარიცხავს 50%-ს, მაშინ წლის ბოლოს არსებული თანხა (1.00+50%)+50% = 1.00×(1+1/2)² = 2.25 ლარი იქნება; თუ დარიცხვა თვეში ოთხჯერ, თითოჯერ 25%, მოხდება, მაშინ სულ 1.00×(1+1/4)⁴ = 2.4414 ლარი დაგროვდება; ყოველთვიურად 8 1/3%-ის დარიცხვით $1.00×(1+1/12)¹²=2.613035... ლარი მიიღება.

ბერნულიმ შენიშნა, რომ დარიცხვის ინტერვალის შემცირებით ეს მიმდევრობა ზღვარს უახლოვდება. ყოველკვირეული დარიცხვით 2.692597… ლარი გამომუშავდება, ყოველდღიური დარიცხვით კი — 2.714567…. თუ დარიცხვების რაოდენობას n-ით აღვნიშნავთ ისე, რომ თითოეულ ინტერვალზე 100%/n დაირიცხოს, ზღვარი n-ის უსასრულოდ დიდი მნიშვნელობებისთვის გარკვეული რიცხვი იქნება; ეს რიცხვი შემდგომში სწორედ e აღმოჩნდა. უწყვეტი დარიცხვის შემთხვევაში, ანგარიშზე 2.7182818… ლარი აღმოჩნდება. ზოგადად, ანგარიში რომელიც 1 ლარით იხსნება და მარტივი პროცენტის დარიცხვის წესით (1+R) ლარს გამოიმუშავებს, უწყვეტი დარიცხვის შემთხვევაში e^R ლარს გამოიმუშავებს.

ბერნულის სქემა

რიცხვი e ალბათობის თეორიაშიც გამოიყენება. დავუშვათ, ადამიანი სათამაშო აპარატით თამაშობს. აპარატით მოგების შანსი 1/n-ია და მოთამაშე აპარატს ზუსტად n-ჯერ იყენებს. მაშინ, n-ის დიდი მნიშვნელობებისთვის (მაგ., n=1 000 000), არაფრის მოგების შანსი დაახლოებით 1/e-ია.

ეს ბერნულის სქემის მაგალითია. ყოველ თამაშზე მოგების შანსი ერთი მემილიონედია. მილიონი ცდიდან k-ჯერ მოგების ალბათობაა

${\binom {10^{6}}{k}}\left(10^{-6}\right)^{k}(1-10^{-6})^{10^{6}-k},$

არც ერთხელ მოგების ალბათობა (k=0) კი იქნება

$\left(1-{\frac {1}{10^{6}}}\right)^{10^{6}}.$

რაც ძალიან ახლოსაა ზღვართან

${\frac {1}{e}}=\lim _{n\to \infty }\left(1-{\frac {1}{n}}\right)^{n}.$

ასიმპტოტური ანალიზი

მუდმივა e ასიმპტოტურ ანალიზშიც გვხვდება. აღსანიშნავია სტირლინგის ფორმულა, რომელშიც რიცხვი e და π გვხვდება:

$n!\sim {\sqrt {2\pi n}}\,{\frac {n^{n}}{e^{n}}}.$

e კალკულუსში

ნატურალურო ლოგარითმის მნიშვნელობა e-ზე, ln(e), 1-ის ტოლია

e-ს ცალკეულ მათემატიკურ მუდმივად შემოღება მაჩვენებლიანი ფუნქციისა და ლოგარითმის გაწარმოებითა და ინტეგრირებით იყო მოტივირებული. ზოგადი მაჩვენებლიანი ფუნქციის a^x-ის წარმოებულს შემდეგი ფორმა აქვს:

${\frac {d}{dx}}a^{x}=\lim _{h\to 0}{\frac {a^{x+h}-a^{x}}{h}}=\lim _{h\to 0}{\frac {a^{x}a^{h}-a^{x}}{h}}=a^{x}\left(\lim _{h\to 0}{\frac {a^{h}-1}{h}}\right).$

მარჯვნივ მოცემული ზღვრის მნიშვნელობა არაა დამოკიდებული x-ზე. ისე ფუძე a-ზეა დამოკიდებული, და როდესაც a=e, ზღვრის მნიშვნელობა 1-ია. მაშასადამე, სიმბოლურად რიცხვი e ასე განისაზღვრება:

${\frac {d}{dx}}e^{x}=e^{x}.$

შესაბამისად, კალკულუსში ფუძე e-ს მქონე მაჩვენებლიანი ფუნქცია მეტად საჭიროა. ფუძედ ამ მუდმივის არჩევა ამარტივებს მაჩვენებლიანი ფუნქციის წარმოებულთან მუშაობას. e-ს მუდმივად დამკვიდრების მეორე მოტივაცია ლოგარითმთანაა დაკავშირებული, როდესაც log_ax-ის წარმოებულს ზღვრის სახით განვმარტავთ:

${\frac {d}{dx}}\log _{a}x=\lim _{h\to 0}{\frac {\log _{a}(x+h)-\log _{a}(x)}{h}}={\frac {1}{x}}\left(\lim _{u\to 0}{\frac {1}{u}}\log _{a}(1+u)\right),$

(სადაც u=h/x). მარჯვენა ზღვრის მნიშვნელობა კვლავ ფუძე a-ზეა დამოკიდებული და როდესაც a=e, ზღვარი 1-ის ტოლია. ასე რომ,

${\frac {d}{dx}}\log _{e}x={\frac {1}{x}}.$

ამ განსაკუთრებულ ფუძიან ლოგარითმს ნატურალური ლოგარითმი ჰქვია და აღინიშნება „ln“ ან „log“ (ეს უკანასკნელი ზოგჯერ ათობითი ლოგარითმის აღსანიშნადაც გამოიყენება). ნატურალურ ლოგარითმის გაწარმოებასთან დაკავშირებული გამოთვლებიც მეტად გამარტივებულია.

მაშასადამე, რიცხვი e=a შეგვიძლია ორი გზით მივიღოთ: 1) გავუტოლოთ მაჩვენებლიანი ფუნქციის a^x წარმოებული a^x-ს; 2) გავუტოლოთ ფუძე a-ს მქონე ლოგარითმის წარმოებული 1/x-ს. ცხადია, მაჩვენებლიან ფუნქციასა და ნატურალურ ლოგარითმს ერთი ფუძე აქვთ — ესაა რიცხვი e.

განსაზღვრებები

ფართობი x-ღერძსა და y = 1/x-ს შორის შუალედზე 1 ≤ x ≤ e 1-ის ტოლია.

რიცხვი e მრავალნაირად შეიძლება წარმოვადგინოთ.

1. e არის ერთადერთი დადებითი ნამდვილი რიცხვი, რომლისთვისაც

${\frac {d}{dt}}e^{t}=e^{t}.$

2. e არის ერთადერთი დადებითი ნამდვილი რიცხვი, რომლისთვისაც

${\frac {d}{dt}}\log _{e}t={\frac {1}{t}}.$

e-ს ეს ორი განსაზღვრება ეკვივალენტურია.

3. e წარმოადგენს ზღვარს

$e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$

ანუ,

$e=\lim _{x\to 0}\left(1+x\right)^{1/x}$

4. e უსასრულო მწკრივის ჯამის ტოლია:

$e=\sum _{n=0}^{\infty }{\frac {1}{n!}}={\frac {1}{0!}}+{\frac {1}{1!}}+{\frac {1}{2!}}+{\frac {1}{3!}}+{\frac {1}{4!}}+\cdots$,

სადაც n! არის n-ის ფაქტორიალი.

5. e ერთადერთი დადებითი ნამდვილი რიცხვია, რომლისთვისაც

$\int _{1}^{e}{\frac {1}{t}}\,dt={1}$.

თვისებები

კალკულუსი

მაჩვენებლიანი ფუნქცია e^x უნიკალური არატრივიალური ფუნქციაა (მუდმივაზე გამრავლებამდე), რომელიც საკუთარი თავის წარმოებულია:

${\frac {d}{dx}}e^{x}=e^{x}$

მაჩვენებლიანი ფუნქციის ანტიწარმოებულიც საკუთარი თავია:

$e^{x}=\int _{-\infty }^{x}e^{t}\,dt$

$=\int _{-\infty }^{0}e^{t}\,dt+\int _{0}^{x}e^{t}\,dt$

$\qquad =1+\int _{0}^{x}e^{t}\,dt.$

ერთ-ერთი ფორმულა, რომელიც e-ს π-ისთან აკავშირებს, ე.წ. „პუასონის ინტეგრალი“ ანუ „გაუსის ინტეგრალია“:

$\int \limits _{-\infty }^{\infty }\ e^{-x^{2}}{dx}={\sqrt {\pi }}$

სხვა ფუნქციები

ფუნქციის

$f(x)={\sqrt[{x}]{x}}$

გლობალური მაქსიმუმი x=e-ს შეესაბამება. x=1/e-ზე კი დადებითი x-ისთვის განსაზღვრული ფუნქცია

$f(x)=x^{x}\,$

აღწევს გლობალურ მინიმუმს. ზოგადად, დადებითი n-ისთვის, $x=e^{-1/n}$ წარმოადგენს

$\!\ f(x)=x^{x^{n}}$

ფუნქციის გლობალურ მინიმუმს. ტეტრაცია

$x^{x^{x^{\cdot ^{\cdot ^{\cdot }}}}}$ ან ^∞$x$

სასრულ მნიშვნელობას იღებს მაშინ, და მხოლოდ მაშინ, როდესაც e^−e ≤ x ≤ e^1/e. ეს ლეონარდ ეილერის თეორემიდან გამომდინარეობს.

რიცხვთა თეორია

რიცხვი e ირაციონალური და ტრანსცენდენტურია (ლინდემან-ვაიერშტრასის თეორემის პირდაპირი შედეგი). ისაა პირველი რიცხვი, რომლის ტრანსცენდენტურობა დაამტკიცეს და ლიუვილის რიცხვისგან განსხვავებით უშუალოდ ამ მიზნით არ გამოუგონიათ. e-ს ტრანსცენდენტურობა შარლ ერმიტმა 1873 წელს დაადგინა. უცნობია, არის თუ არა e რომელიმე ფუძისთვის ნორმალური რიცხვი.

კომპლექსური რიცხვები

მაჩვენებლიანი ფუნქცია e^x ტეილორის მწკრივის სახით ასე ჩაიწერება:

$e^{x}=1+{x \over 1!}+{x^{2} \over 2!}+{x^{3} \over 3!}+\cdots =\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}$

ეს მწკრივი ხშირად კომპლექსურ რიცხვებზე განივრცობა. ნებისმიერი კომპლექსური z-ისთვის სამართლიანია ტოლობა

$e^{z}=\sum _{n=0}^{\infty }{\frac {1}{n!}}z^{n}=\lim _{n\to \infty }\left(1+{\frac {z}{n}}\right)^{n}.$

მაჩვენებლიანი ფუნქციის, სინუსისა და კოსინუსის ტეილორის მწკრივებად გაშლის მეშვეობით მტკიცდება ეილერის ფორმულა:

$e^{ix}=\cos x+i\sin x,\,\!$

რომელიც ნებისმიერი x-ისთვისაა სამართლიანი. როდესაც x=π, ვიღებთ ეილერის იგივეობას:

$e^{i\pi }=-1\,\!$

ახარისხების წესებიდან გამომდინარეობს, რომ

$(\cos x+i\sin x)^{n}=\left(e^{ix}\right)^{n}=e^{inx}=\cos(nx)+i\sin(nx),$

ეს მუავრის ფორმულაა. შემთხვევა

$\cos(x)+i\sin(x)\,\!$

ხანდახან გამოისახება, როგორც Cis(x).

დიფერენციალური განტოლებები

ზოგადი ფუნქცია

$y(x)=Ce^{x}\,$

არის

$y'=y.\,$

დიფერენციალური განტოლების ამონახსნი.

e-ს სხვადასხვა ფორმით გამოსახვა

უსასრულო მწკრივის ჯამის სახით

$e=\sum _{n=0}^{\infty }{\frac {1}{n!}}$ (მაჩვენებლიანი ფუნქციის ტეილორის მწკრივის კერძო შემთხვევა x=1-ისთვის)

ასევე:

$e=\left[\sum _{k=0}^{\infty }{\frac {1-2k}{(2k)!}}\right]^{-1}$

$e={\frac {1}{2}}\sum _{k=0}^{\infty }{\frac {k+1}{k!}}$

$e=2\sum _{k=0}^{\infty }{\frac {k+1}{(2k+1)!}}$

$e=\sum _{k=0}^{\infty }{\frac {3-4k^{2}}{(2k+1)!}}$

$e=\sum _{k=0}^{\infty }{\frac {(3k)^{2}+1}{(3k)!}}$

$e=\left[\sum _{k=0}^{\infty }{\frac {4k+3}{2^{2k+1}\,(2k+1)!}}\right]^{2}$

$e=-{\frac {12}{\pi ^{2}}}\left[\sum _{k=1}^{\infty }{\frac {1}{k^{2}}}\ \cos \left({\frac {9}{k\pi +{\sqrt {k^{2}\pi ^{2}-9}}}}\right)\right]^{-1/3}$

$e=\sum _{k=1}^{\infty }{\frac {k^{n}}{B_{n}(k!)}}$, სადაც $B_{n}$ არის მე-$n$ ბელის რიცხვი (მაგალითები: n=1,2,3).

$e=\sum _{k=1}^{\infty }{\frac {k}{k!}}=\sum _{k=1}^{\infty }{\frac {1}{(k-1)!}}=\sum _{k=0}^{\infty }{\frac {1}{k!}}$

$e={\frac {1}{2}}\sum _{k=1}^{\infty }{\frac {k^{2}}{k!}}$

$e={\frac {1}{5}}\sum _{k=1}^{\infty }{\frac {k^{5}}{k!}}$

უწყვეტი წილადის სახით

e შეიძლება ჩაიწეროს, როგორც უწყვეტი მარტივი უწყვეტი წილადი:

$e=2+{\cfrac {1}{1+{\cfrac {1}{{\mathbf {2} }+{\cfrac {1}{1+{\cfrac {1}{1+{\cfrac {1}{{\mathbf {4} }+{\cfrac {1}{1+{\cfrac {1}{1+\ddots }}}}}}}}}}}}}}$

ამ წილადის უფრო კომპაქტური ფორმაა

$e=[[2;1,{\textbf {2}},1,1,{\textbf {4}},1,1,{\textbf {6}},1,1,{\textbf {8}},1,1,\ldots ,{\textbf {2n}},1,1,\ldots ]],\,$

სამჯერ უფრო სწრაფად უახლოვდება e-ს ზუსტ მნიშვნელობას (არამარტივი) უწყვეტი წილადი

$e=[1,{\textbf {0.5}},12,5,28,9,44,13,60,17,\ldots ,{\textbf {4(4n-1)}},{\textbf {4n+1}},\ldots ].\,$

ნულის ჩამატებით ვიღებთ

$e=[[1,{\textbf {0}},1,1,{\textbf {2}},1,1,{\textbf {4}},1,1,{\textbf {6}},1,1,{\textbf {8}},1,1,\ldots ]].\,$

e ზოგადი უწყვეტი წილადის სახითაც ჩაიწერება:

$e=2+{\cfrac {1}{1+{\cfrac {1}{2+{\cfrac {2}{3+{\cfrac {3}{4+{\cfrac {4}{5+\ddots }}}}}}}}}}\qquad e=2+{\cfrac {2}{2+{\cfrac {3}{3+{\cfrac {4}{4+{\cfrac {5}{5+{\cfrac {6}{6+\ddots \,}}}}}}}}}}$

$e=1+{\cfrac {2}{1+{\cfrac {1}{6+{\cfrac {1}{10+{\cfrac {1}{14+{\cfrac {1}{18+\ddots \,}}}}}}}}}}$

უსასრულო ნამრავლის სახით

კატალანმა e გამოსახა, როგორც

$e=2\cdot {\sqrt {\frac {4}{3}}}\cdot {\sqrt[{4}]{\frac {6\cdot 8}{5\cdot 7}}}\cdot {\sqrt[{8}]{\frac {10\cdot 12\cdot 14\cdot 16}{9\cdot 11\cdot 13\cdot 15}}}\cdots$

პიპენგერის ნამრავლია

$e=2\left({\frac {2}{1}}\right)^{1/2}\left({\frac {2}{3}}\;{\frac {4}{3}}\right)^{1/4}\left({\frac {4}{5}}\;{\frac {6}{5}}\;{\frac {6}{7}}\;{\frac {8}{7}}\right)^{1/8}\cdots$

გილერას ნამრავლია

$e=\left({\frac {2}{1}}\right)^{1/1}\left({\frac {2^{2}}{1\cdot 3}}\right)^{1/2}\left({\frac {2^{3}\cdot 4}{1\cdot 3^{3}}}\right)^{1/3}\left({\frac {2^{4}\cdot 4^{4}}{1\cdot 3^{6}\cdot 5}}\right)^{1/4}\cdots ,$

სადაც მე-n თანამამრავლი

$\prod _{k=0}^{n}(k+1)^{(-1)^{k+1}{n \choose k}},$

ნამრავლის მე-n ფესვია. გარდა ამისა,

$e={\frac {2\cdot 2^{(\ln(2)-1)^{2}}\cdots }{2^{\ln(2)-1}\cdot 2^{(\ln(2)-1)^{3}}\cdots }}.$

მიმდევრობის ზღვრის სახით

რიცხვი e რამდენიმე უსასრულო მიმდევრობის ზღვარია.

$e=\lim _{n\to \infty }n\cdot \left({\frac {\sqrt {2\pi n}}{n!}}\right)^{1/n}$ და

$e=\lim _{n\to \infty }{\frac {n}{\sqrt[{n}]{n!}}}$ (ორივე გამოსახულება სტირლინგის ფორმულის შედეგია).

სიმეტრიული ზღვარი

$e=\lim _{n\to \infty }\left[{\frac {(n+1)^{n+1}}{n^{n}}}-{\frac {n^{n}}{(n-1)^{n-1}}}\right]$

e-ს ძირითადი ზღვრის სახით განმარტების, $e=\lim _{n\to \infty }\left(1+{\frac {1}{n}}\right)^{n}$, მანიპულაციით მიიღება. დამატებით,

$e=\lim _{n\to \infty }(p_{n}\sharp )^{1/p_{n}}$

სადაც $p_{n}$ მე-n მარტივი რიცხვია, $p_{n}\sharp$ კი — პირველი n მარტივი რიცხვის ნამრავლი.

e-ს ციფრები

e-ს ცნობილი ციფრების რაოდენობა ბოლო წლებში დიდად გაიზარდა, რაც ძლიერი კომპიუტერებისა და ალგორითმების დამსახურებაა.

e-ს ცნობილი ციფრების რაოდენობა

თარიღი	ციფრი	გამოთვლის ავოტრი
1748	18	ლეონარდ ეილერი
1853	137	უილიამ შენკსი
1871	205	უილიამ შენკსი
1884	346	ჯ. მარკუს ბურმენი
1946	808	უცნობი
1949	2 010	ჯონ ფონ ნოიმანი (ENIAC-ზე)
1961	100 265	დანიელ შენკსი და ჯონ რენჩი
1978	116 000	სტივენ გ. ვოზნიაკი (Apple II-ზე)
1994	10 000 000	რობერტ ნემიროვი და ჯერი ბონელი
მაისი, 1997	18 199 978	პატრიკ დემიშელი
აგვისტო, 1997	20 000 000	ბირგერ სეიფერტი
სექტემბერი, 1997	50 000 817	პატრიკ დემიშელი
თებერვალი, 1999	200 000 579	სებასტიან ვედენივსკი
ოქტომბერი, 1999	869 894 101	სებასტიან ვედენივსკი
21 ნოემბერი, 1999	1 250 000 000	ხავიერ გორდონი
10 ივლისი, 2000	2 147 483 648	შიგერუ კონდო და ხავიერ გორდონი
16 ივლისი, 2000	3 221 225 472	კოლინ მარტინი და ხავიერ გორდონი
2 აგვისტო, 2000	6 442 450 944	შიგერუ კონდო და ხავიერ გორდონი
16 აგვისტო, 2000	12 884 901 000	შიგერუ კონდო და ხავიერ გორდონი
21 აგვისტო, 2003	25 100 000 000	შიგერუ კონდო და ხავიერ გორდონი
18 სექტემბერი, 2003	50 100 000 000	შიგერუ კონდო და ხავიერ გორდონი
27 აპრილი, 2007	100 000 000 000	შიგერუ კონდო და სტივ პაგლიარულო
6 მაისი, 2009	200 000 000 000	შიგერუ კონდო და სტივ პაგლიარულო
21 თებერვალი, 2010	500 000 000 000	ალექსანდრ ჯ. ი

ირაციონალურობის დამტკიცება

დავუშვათ, e რაციონალურია. მაშინ $\!e=p/q$, სადაც $\!p$ მთელი რიცხვია, $\!q$ კი — ნატურალურია და 1-ს აღემატება, რადგან e არაა მთელი რიცხვი. მაშასადამე,

$\!p=eq$

განტოლების ორივე მხარის $\!(q-1)!$-ზე გამრავლებით ვიღებთ, რომ

$p(q-1)!=eq!=q!\sum _{n=0}^{\infty }{1 \over n!}=\sum _{n=0}^{\infty }{q! \over n!}=\sum _{n=0}^{q}{q! \over n!}+\sum _{n=q+1}^{\infty }{q! \over n!}$

$\sum _{n=0}^{q}{q! \over n!}$-ის მარცხნივ გადატანით ვიღებთ:

$\sum _{n=q+1}^{\infty }{q! \over n!}=p(q-1)!-\sum _{n=0}^{q}{q! \over n!}$

განტოლების მარჯვენა მხარეს არსებული ყველა სიდიდე მთელია. მაშასადამე

$\sum _{n=q+1}^{\infty }{q! \over n!}$ მთელია და

$\sum _{n=q+1}^{\infty }{q! \over n!}\geq 1$

მაგრამ

$\sum _{n=q+1}^{\infty }{q! \over n!}=\sum _{m=1}^{\infty }{q! \over (q+m)!}=\sum _{m=1}^{\infty }{1 \over (q+1)...(q+m)}<\sum _{m=1}^{\infty }{1 \over (q+1)^{m}}={1 \over q}<1$.

მივიღეთ წინააღმდეგობა. მაშასადამე, დაშვება, რომ e რაციონალურია, მცდარია. ე.ი., e ირაციონალურია.

რესურსები ინტერნეტში

• [https://web.archive.org/web/20160304125544/http://math.ge/forum/viewforum.php?f=39&t=85 დაარქივებული 2016-03-04 საიტზე Wayback Machine. ეილერის რიცხვი]