კონუსი

კონუსი

კონუსი (გერმ. Konus და ლათ. cōnus, ძვ. ბერძნ. κώνοςდან — «ფიჭვის გირჩი») — ზედაპირი, წარმოქმნილი სივრცეში მრავალი სხივისაგან (რომლებმაც წარმოქმნეს კონუსი), რომელიც ყველა წერტილს აერთიანებს გარკვეული ბრტყელი მრუდის მიხედვით (კონუსის მიმართულებით) სივრცეში მოცემულ წერტილთან (კონუსის წვერი).

თუ კონუსის მიმმართველი დახურული მრუდია, მაშინ კონუსური ზედაპირი ემსახურება სივრცითი სხეულის საზღვარს, რომელსაც ასევე უწოდებენ „კონუსს“ (იხ. ნახატი), ხოლო ამ მრუდის შიდა ნაწილს უწოდებენ „კონუსის ფუძეს“, თუ კონუსის ფუძე წარმოადგენს მრავალკუთხედს, მაშინ ასეთი კონუსია პირამიდა.

ორმაგი კონუსი

ზოგჯერ სხივების ნაცვლად განიხილება წრფეები, მაშინ მივიღებთ ორმაგ კონუსს, რომელიც შედგება წვეროსთან შეფარდებით ორი სიმეტრიული ნაწილისაგან.

კონუსი და მასთან დაკავშირებული კონუსური ჭრილი დიდ როლს თამაშობს მათემატიკაში, ასტრონომიაში და სხვა მეცნიერებებში.

დაკავშირებული განსაზღვრებები

• კონუსის გვერდითი ზედაპირი — კონუსის შემქმნელთა გაერთიანება.
• კონუსის სიმაღლე — წვეროდან პერპენდიკულარულად დაშვებული მონაკვეთი ფუძის სიბრტყეზე (ასევე ასეთი მონაკვეთის სიგრძე).
• კონუსის ხსნარის კუთხე — კუთხე ორ საპირისპირო წარმომქმნელებს შორის (კუთხე კონუსის წვეროსთან, კონუსის შიგნით).
• კონუსობა — კონუსის ფუძის სიმაღლისა და დიამეტრის თანაფარდობა.

კონუსის ტიპები

• 
  სწორი წრიული კონუსი
• 
  სწორი და ირიბი წრიული კონუსები с თანაბარი ფუძით და სიმაღლით: მათი მოცულობა ერთი და იგივეა
• 
  წაკვეთილი სწორი წრიული კონუსი

• სწორი კონუსი — კონუსი, რომლის ფუძეს აქვს სიმეტრიის ცენტრი (მაგალითად, არის წრე ან ელიფსი) და კონუსის წვეროს ორთოგონალური პროექცია ფუძის სიბრტყეზე ემთხვევა ამ ცენტრს; ამასთან წრფეს, რომელიც აერთებს წვეროს და ფუძის ცენტრს, ეწოდება კონუსის ღერძი.
• ირიბი (ან დახრილი) კონუსი — კონუსი, რომელსაც წვეროს ფუძეზე ორთოგონალური პროექცია არ ემთხვევა მის სიმეტრიის ცენტრს.
• წრიული კონუსი — კონუსი, რომლის ფუძე წრეა.
• ბრუნვადი კონუსი, ან სწორი წრიული კონუსი (ხშირად კონუსი იგულისხმება როგორც წრიული) — კონუსი, რომელიც შეიძლება მივიღოთ მართკუთხა სამკუთხედის ბრუნვით (ანუ ბრუნვადი სხეულები) წრფის გარშემო, რომელსაც გააჩნია სამკუთხედის კათეტი (ეს წრფე კონუსის ღერძია).
• კონუსი, დაყრდნობილი ელიფსზე, პარაბოლაზე ან ჰიპერბოლაზე, შესაბამისად უწოდებენ ელიფსურს, პარაბოლურს და ჰიპერბოლურ კონუსება: უკანასკნელ ორს აქვთ უსასრულო მოცულობა.
• წაკვეთილი კონუსი ან კონუსური ფენა — ფუძესა და სიბრტყეს შორის მყოფი კონუსის ნაწილი, როდესაც სიბრტყე პარალელურია ფუძისა და იმყოფება წვეროსა და ფუძეს შორის.
• ტოლგვერდა კონუსი — ბრუნვადი კონუსი, რომლის წარმომქმნელი ტოლია ფუძის დიამეტრისა.

თვისებები

• თუ ფუძის ფართობი განსაზღვრულია, მაშინ კონუსის მოცულობაც განსაზღვრულია და ტოლია ფუძის ფართობის სიმაღლეზე ნამრავლის მესამედისა.

𝑉 = 1/3𝑆𝐻,

სადაც S — ფუძის ფართობია,  H — სიმაღლე. აქედან გამომდინარე, ყველა კონუსი, რომელიც ეყრდნობა მოცემულ ფუძეს (საბოლოო ფართობი) და აქვთ წვეროები, მდებარეობენ ფუძის პარალელურ მოცემულ სიბრტყეზე, აქვთ ტოლი მოცულობა, რადგანაც მათი სიმაღლეები ტოლია.

• ნებისმიერი კონუსის სიმძიმის ცენტრი საბოლოო მოცულობით ფუძეზე სიმაღლის მეოთხედია.
• სხეულის კუთხე სწორი წრიული კონუსის წვეროსთან ტოლია

2𝜋(1 − cos 𝛼/2),

სადაც α — კონუსის ხსნარის კუთხე.

• სწორი წრიული კონუსის გვერდითი ზედაპირის ფართობი ტოლია

𝑆 = 𝜋𝑅𝑡,

ხოლო საერთო შემთხვევაში

𝑆 = 𝑡𝑙/2,

სადაც R — ფუძის რადიუსია, 𝑡² = 𝑅² + 𝐻² — ფორმირების სიგრძე, 𝑙 — ფუძის საზღვრის სიგრძე.

ზედაპირის მთლიანი ფართობი (ანუ გვერდითი ზედაპირის და ფუძის ფართობების ჯამი) ტოლია

𝑆 = 𝜋𝑅(𝑡 + 𝑅),

სწორი წრიული კონუსისთვის

𝑆 = 𝑡𝑙/2 + 𝑆_ос

და ნებისმიერისთვის, სადაც 𝑆_ос — ფუძის ფართობია.

• წრიული კონუსის (არ არის აუცილებელი სწორი) მოცულობა ტოლია

𝑉 = 1/3𝜋𝑅²𝐻.

• წაკვეთილი წრიული კონუსის (არ არის აუცილებელი სწორი) მოცულობა ტოლია:

𝑉 = 1/3𝜋𝐻(𝑅² + 𝑅_𝑟 + 𝑟²),

სადაც 𝑅 და 𝑟 — შესაბამისი ქვედა და ზედა ფუძის რადიუსებია, 𝐻 — სიმაღლე ქვედა ფუძის სიბრტყიდან ზედა ფუძემდე.

• ნებისმიერი წაკვეთილი კონუსისთვის (არ არის აუცილებელი სწორი ან წრიული) მოცულობა ტოლია:

𝑉 = 1/3(𝐻₂𝑆₂ − 𝐻₁𝑆₁),

სადაც 𝑆₁ და 𝑆₂ — შესაბამისად ზედა (ახლოს მყოფი წვეროსთან) და ქვედა ფუძის ფართობები, 𝐻₁ და 𝐻₂ — მანძილი სიბრტყიდან შესაბამისად ზედა და ქვედა ფუძიდან წვერომდე.

• სიბრტყის გადაკვეთა სწორი წრიული კონუსით არის ერთ-ერთი კონუსური კვეთა (განუვითარებელ შემთხვევებში — ელიფსი, პარაბოლა ან ჰიპერბოლა, კვეთის სიბრტყის პოზიციიდან გამომდინარე).

სწორი წრიული კონუსის განტოლება

განტოლებები, რომლებიც აჩვენებენ სწორი წრიული კოუნუსის გვერდით ზედაპირს კუთხით 2Θ, წვეროსი კოორდინატების დასაწყისში და ღერძით, რომელიც ემთხვევა ღერძ Oz-ს:

• სფერულ კოორდინატთა სისტემაში კოორდინატებით (r, φ, θ):

𝜃 = Θ.

• ცილინდრულ კოორდინატთა სისტემაში კოორდინატებით (r, φ, z):

𝑧 = 𝑟 ⋅ ctg Θ или 𝑟 = 𝑧 ⋅ tg Θ.

• დეკარტის კოორდინატთა სისტემაში კოორდინატებით (x, y, z):

𝑧² = ±(𝑥²+𝑦²) ⋅ ctg² Θ.

ეს განტოლება კანონიკური სახით ჩაიწერება როგორც

𝑥²/𝑎²+𝑦²/𝑎²−𝑧²𝑐² = 0,

სადაც კონსტანტები a, с განისაზღვრება პროპორციით 𝑐/𝑎 = cos Θ/sin Θ. აქედან ჩანს, რომ სწორი წრიული კონუსის გვერდითი ზედაპირი წარმოადგენს მეორე რიგის ზედაპირს (მას ქვია კონუსის ზედაპირი). მეორე რიგის კონუსის ზედაპირი ეყრდნობა ელიფსს; შესაბამის დეკარტის კოორდინატულ სისტემაში (ღერძები Ох და Оу პარალელურები არიან ელიფსის ღერძებთან, კონუსის წვერი ემთხვევა კოორდინატების საწყისს, ელიფსის ცენტრი დევს Oz-ის ღერძზე) მის განტოლებას აქვს შემდეგი სახე

𝑥²/𝑎²+𝑦²/𝑏²−𝑧²/𝑐² = 0,

თანაც a/c და b/c ტოლია ელიფსის ნახევარღერძების. ყველაზე უფრო საერთო შემთხვევაში, როდესაც კონუსი ეყრდნობა თავისუფალ ბრტყელ ზედაპირს, შეიძლება ითქვას, რომ კონუსის გვერდითი ზედაპირის ტოლობა (წვეროთი კოორდინატების დასაწყისში) ამოიხსნება განტოლებით 𝑓(𝑥,𝑦,𝑧)=0, სადაც ფუნქცია 𝑓(𝑥,𝑦,𝑧) არის ერთგვაროვანი, ანუ აკმაყოფილებს პირობას 𝑓(𝛼𝑥,𝛼𝑦,𝛼𝑧) = 𝛼ⁿ𝑓(𝑥,𝑦,𝑧) ნებისმიერი მოქმედი α რიცხვისთვის.

გაშლა

სწორი წრიული კონუსის გაშლა

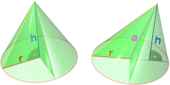
სწორი წრიული კონუსი, როგორც მბრუნავი სხეული შეიქმნა მართკუთხა სამკუთხედისაგან, რომელიც ბრუნავს ერთ-ერთი კათეტის გარშემო, სადაც h — კონუსის სიმაღლეა ფუძის ცენტრიდან წვერომდე და არის კათეტი მართკუთხა სამკუთხედისა, რომლის გარშემო ხდება ბრუნვა. მართკუთხა სამკუთხედის მეორე კათეტია r — კონუსის ფუძის რადიუსი. მართკუთხა სამკუთხედის ჰიპოტენუზა არის l — კონუსის შემქმნელი.

კონუსის გაშლის შექმნაში შეიძლება გამოვიყენოთ მხოლოდ ორი სიდიდე r და l. ფუძის რადიუსი r გაშლაში განსაზღვრავს კონუსის ფუძის წრეს, ხოლო კონუსის გვერდითი ზედაპირის სექტორს განსაზღვრავს გვერდითი ზედაპირის წარმომქნელი l, რომელიც გვერდითი ზედაპირის სექტორის რადიუსია. სექტორის კუთხე 𝜑 კონუსის გვერდითი ზედაპირის გაშლაში განისაზღვრება ფორმულით:

φ = 360°·(r/l).

ვარიაციები და განზოგადებები

• ალგებრალურ გეომეტრიაში კონუსი ეს არის 𝑉 ვექტორული სივრცის ნებისმიერი 𝐾 ქვეკგუფი 𝐹 მინდორზე, რომლისთვისაც ნებისმიერი 𝜆 ∈ 𝐹

𝜆𝐾=𝐾.

• ტოპოლოგიაში კონუსი X ტოპოლოგიურ სივრცეზე არის 𝑋×[0,∞) ფაქტორსივრცე (𝑥,0)∼(𝑦,0) ეკვივალენტობასთან მიმართებაში.

• ხაზოვან ალგებრაში არსებობს ცნება ამოზნექილი კონუსი.