ელიფსი

სიბრტყის მიერ კონუსის კვეთით მიღებული გეომეტრიული ფიგურები: წრეწირი, ელიფსი, პარაბოლა, ჰიპერბოლა

ელიფსი (ძვ. ბერძნ. ἔλλειψις [elleipsis] — „ნაკლი“, „დანაკლისი“) — წრიული კონუსის გადაკვეთის წირი სიბრტყესთან, რომელიც კვეთს ამ კონუსის ერთ-ერთი კალთის ყველა მსახველს.

ელიფსის თვისებები

ელიფსი და მისი თვისებები

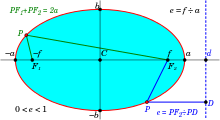
ელიფსი შეიძლება განისაზღვროს აგრეთვე როგორც სიბრტყის იმ $P$ წერტილთა გეომეტრიული ადგილი, რომელთათვის ამ სიბრტყის ორ მოცემულ $F_{1}$ და $F_{2}$ წერტილებამდე (ელიფსის ფოკუსებამდე) მანძილების ჯამი მუდმივი სიდიდეა. თუ კოორდინატთა სისტემას ავირჩევთ ისე, როგორც ეს ნაჩვენებია ნახაზზე ($OF_{1}=OF_{2}=c$), მაშინ ელიფსის განტოლება მიიღებს შემდეგ სახეს: $\left({\frac {x}{a}}\right)^{2}+\left({\frac {y}{b}}\right)^{2}=1(2a=F_{1}P+F_{2}P)$; $a=OA$ და $b=OC$, ე. წ. ელიფსის დიდი მდა მცირე ნახევარღერძებია. ვინაიდან ელიფსის განტოლება მეორე ხარისხისაა, ელიფსი მეორე რიგის წირია. როდესაც $a=b$, მაშინ ელიფსი გადაიქცევა წრეწირად. სიდიდეს $e=c/a$, სადაც $c={\sqrt {a^{2}-b^{2}}}$, ეწოდება ელიფსის ექსცენტრისიტეტი, რომელიც ერთზე ნაკლებია. იგი ახასიათებს ელიფსის გაჭიმულობას.

ანალიზურ გეომეტრიაში, ელიფსი განმარტებულია, როგორც დეკარტის კოორდინატთა სისტემაში არსებული (X,Y) წერტილთა სიმრავლე, რომლებიც აკმაყოფილებენ შემდეგ ტოლობას:

$Ax^{2}+Bxy+Cy^{2}+Dx+Ey+F=0$

სადაც $B^{2}<4AC$, ფუნქციის ყველა კოეფიციენტი ნამდვილი რიცხვია და არსებობს ერთზე მეტი ამომხსნელი, განსაზღვრული ელიფსზე მდებარე (x, y) წერტილთა წყვილებით.

იხილეთ აგრეთვე

• ანალიზური გეომეტრია
• კონუსური კვეთა
• წრეწირი
• ჰიპერბოლა
• პარაბოლა

ლიტერატურა

• Besant, W.H. (1907). „Chapter III. The Ellipse“, Conic Sections. London: George Bell and Sons, გვ. 50. 
• Coxeter, H.S.M. (1969). Introduction to Geometry, 2nd, New York: Wiley, გვ. 115–9. 
• Meserve, Bruce E. (1983), Fundamental Concepts of Geometry, Dover, ISBN 0-486-63415-9
• (1990) Fundamentals of College Algebra, 3rd, Scott Foresman/Little, გვ. 381. ISBN 0-673-38638-4. 

რესურსები ინტერნეტში

• Draw A Perfect Ellipse YouTube-ზე