დიპოლი

ფიზიკაში არსებობს ორი სახის დიპოლი:
- ელექტრული დიპოლი — სისტემა, რომელიც შედგენილია გარკვეული მანძილებით დაშორებული ელექტრული მუხტებისგან. დიპოლის უმარტივესი მაგალითია შედარებით მცირე მანძილით დაშორებული ორი სიდიდით ტოლი და ნიშნით საპირისპირო მუხტისგან შედგენილი სისტემა.
- მაგნიტური დიპოლი შეიძლება შეიქმნას ელექტრული დენის ცირკულაციის შედეგად. მაგნიტური დიპოლის უმარტივესი მაგალითია გამტარის ერთი მარყუჟი, რომელშიც მუდმივი დენი გადის.[1][2]
დიპოლი ხასიათდება დიპოლური მომენტით, რომელიც ვექტორული სიდიდეა. ზემოთ აღწერილი უმარტივესი ელექტრული დიპოლისთვის ელექტრული დიპოლური მომენტი არის ვექტორი, რომელიც მიმართულია უარყოფითი მუხტიდან დადებითი მუხტისკენ, ხოლო მისი სიდიდე დადებით მუხტსა და მუხტებს შორის მანძილის ნამრავლის ტოლია. დენიანი მარყუჟისთვის მაგნიტური დიპოლური მომენტი მიმართულია მარყუჟის სიბრტყის მართობულად (მარჯვენა ხელის წესის მიხედვით), ხოლო მისი სიდიდე მარყუჟში გამავალი დენისა და გამტარით შომოფარგლული ფართის ნამრავლის ტოლია.


მაგნიტური დიპოლის ველი[რედაქტირება | წყაროს რედაქტირება]
სიდიდე[რედაქტირება | წყაროს რედაქტირება]
დიპოლიდან შორ მანძილზე დიპოლური მაგნიტური ველის ინდუქცია B მოიცემა შემდეგი გამოსახულებით
სადაც
- B არის მაგნიტური ინდუქცია ტესლებში
- r არის დაშორება დიპოლის ცენტრიდან მეტრებში
- λ არის მაგნიტური განედი (რომელიც 90° − θ-ს ტოლია) სადაც θ არის მაგნიტური თანაგანედი , რომელიც იზომება რადიანებში. თანაგანედი 0-ის ტოლია დიპოლის ღერძის გასწვრივ და 90°-ის ტოლია დიპოლის ღერძის მართობულ სიბრტყეში.
- m არის მაგნიტური დიპოლური მომენტი, ამპერი კვადრატულ მეტრზე ერთეულებში (A·m2).
- μ0 არის მაგნიტური მუდმივა.
ცილინდრულ კოორდინატებში ამ ფორმულის გადაყვანა ხდება და
ფორმულების მეშვეობით, სადაც ρ არის წერტილის დაშორება (დიპოლის პარალელური) z-ღერძიდან. საბოლოდდ მივიღებთ
ვექტორული ფორმა[რედაქტირება | წყაროს რედაქტირება]
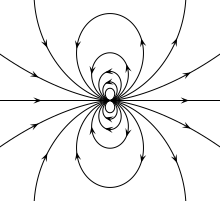
მაგნიტური ინდუქცია ვექტორული სიდიდეა, რომლისთვისაც გვაქვს:
სადაც
- B არის მაგნიტური ინდუქცია;
- r არის ვექტორი დიპოლის ცენტრიდან გაზომვის წერტილამდე;
- r არის r-ის აბსოლუტური მნიშვნელობა, ანუ მანძილი დიპოლის ცენტრიდან გაზომვის წერტილამდე;
- არის r-ის გასწვრივ მიმართული ერთეულოვანი ვექტორი;
- m არის (ვექტორული) [[მაგნიტური დიპოლური მომენტი;
- μ0 არის მაგნიტური მუდმივა;
- δ3 არის სამგანზომილებიანი დირაკის დელტა ფუნქცია.
მოცემული ფურმულა არის ზუსტი წერტილოვანი დიპოლისთვის, ასევე ზუსტად აღწერს ნებისმიერი ველის მულტიპოლური გაშლის დიპოლურ წევრს, და დაახლოებით სამართლიანია დიპოლური კონფიგურაციების ველების განსაზღვრისათვის შორ მანძილებზე (ისეთ მანძილებზე, რომლებიც დიპოლური სისტემის ზომაზე გაცილებით მეტია).
მაგნიტური ვექტორული პოტენციალი[რედაქტირება | წყაროს რედაქტირება]
მაგნიტური დიპოლის ვექტორული პოტენციალი A მოიცემა შემდეგი ფორმულით
- .
დიპოლური გამოსხივება[რედაქტირება | წყაროს რედაქტირება]

სტატიკური დიპოლების გარდა ხშირად განიხილავენ მერხევ ელექტრულ და მაგნიტურ დიპოლებს.
სახელდობრ, ჰარმონიულად მერხევი ელექტრული დიპოლი აღიწერება შემდეგი სახის დიპოლური მომენტით
სადაც ω არის კუთხური სიხშირე. ასეთი დიპოლის გენერირებულ ველს აქვს სახე:
შორ მანძილებზე (ანუ როდესაც ), ელექტრული ველი უახლოვდება სფერული ტალღას:
რომლის დროში გასაშუალოებული გამოსხივების სიმძლავრე P მოიცემა ფორმულით
ეს სიმძლავრე არ ნაწილდება იზოტროპულად, არამედ გამოსხივდება უპირატესად დიპოლური მომენტის მართობი მიმართულებით.
იხილეთ აგრეთვე[რედაქტირება | წყაროს რედაქტირება]
სქოლიო[რედაქტირება | წყაროს რედაქტირება]
- ↑ Brau, Charles A. (2004). Modern Problems in Classical Electrodynamics. Oxford University Press. ISBN 0-19-514665-4.
- ↑ Griffiths, David J. (1999). Introduction to Electrodynamics, 3rd, Prentice Hall. ISBN 0-13-805326-X.








![{\displaystyle \mathbf {E} ={\frac {1}{4\pi \varepsilon _{0}}}\left\{{\frac {\omega ^{2}}{c^{2}r}}{\hat {\mathbf {r} }}\times \mathbf {p} \times {\hat {\mathbf {r} }}+\left({\frac {1}{r^{3}}}-{\frac {i\omega }{cr^{2}}}\right)\left[3{\hat {\mathbf {r} }}({\hat {\mathbf {r} }}\cdot \mathbf {p} )-\mathbf {p} \right]\right\}e^{i\omega r/c}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e0ad1f0c20dbaee5c2469392d307662cf2726f5d)




