გრავიტაციული ლინზირება

გრავიტაციული ლინზირება ხდება, როდესაც სივრცეში განაწილებული მატერია (როგორიცაა გალაქტიკური გროვა) ექცევა შორეულ წყაროსა (უკან მყოფი გალაქტიკა) და დამკვირვებელს შორის. ამ მატერიას შესწევს იმის უნარი, რომ სინათლე დაამახინჯოს, ანუ მოახდინოს მისი ლინზირება, როდესაც სინათლე დამკვირვებლისკენ მოდის. ეს ეფექტი ცნობილია, როგორც გრავიტაციული ლინზირება, რადგან ამ დროს ხდება ისეთივე ლინზირება, როგორსაც ჩვეულებრივი ოპტიკური ლინზა აკეთებს. ეს მოვლენა ალბერტ აინშტაინმა თავის ფარდობითობის ზოგად თეორიაში იწინასწარმეტყველა. თუმცა, მიჩნეულია, რომ ორესტ ჩუოლსონმა წამოაყენა პირველად თეორია ამ ეფექტის შესახებ 1924 წელს, მაგრამ გრავიტაციული ლინზირება მაინც უფრო აინშტაინთან ასოცირდება, რომელმაც გამოაქვეყნა უფრო ცნობილი სტატია ამ მოვლენაზე 1936 წელს.
აღწერა[რედაქტირება | წყაროს რედაქტირება]
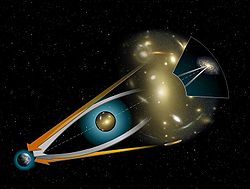


მასიური ობიექტის (მაგალითად გალაქტიკური გროვის ან შავი ხვრელის) გარშემო დრო-სივრცე გამრუდებულია. შედეგად, უკან მყოფი წყაროდან (მაგ. გალაქტიკა) წამოსული სინათლე დრო-სივრცეში გავლისას მრავლდება და დეფორმირდება. გრავიტაციულ ლინზირებას ასევე შესწევს იმის ძალა, რომ უკან მყოფი ობიექტი გაადიდოს ან დეფორმირება მოახდინოს.
ოპტიკური ლინზისაგან განსხვავებით, მაქსიმალური დეფორმაცია მაშინ ხდება, როდესაც ობიექტი „ლინზასთან“ ახლოსაა და პირიქით, რაც უფრო შორსაა მით უფრო ნაკლებად ლინზირდება ობიექტი. მაშასადამე, გრავიტაციულ ლინზას არ აქვს ერთი ფოკუსური მანძილი, მაგრამ ამის ნაცვლად აქვს ფოკუსური ხაზი. თუ სინათლის წყარო (რომელსაც ვაკვირდებით) გრავიტაციული ლინზა (მასიური ობიექტი) და დამკვირვებელი ერთ სწორ ხაზზე აღმოჩნდენ, თავდაპირველი სინათლის წყარო გამოჩნდება, თითქოს მასიური ლინზის გარშემო დიდი რგოლია. თუ არასწორი განლაგებაა (ანუ ზუსტად ერთ ხაზზე არ არიან განლაგებულნი), მაშინ დამკვირვებელი რგოლის ნაცვლად დაინახავს ლინზირებულ რკალს. ეს ფენომენი პირველად ახსენა სანქტ-პეტერბურგის ფიზიკოსმა ორესტ ჩოულსონმა, ხოლო 1936 წელს ალბერტ აინშტაინმა ზუსტად განსაზღვრა. სადაც გრავიტაციული ლინზის მასა არის არათანაბარი ( ანუ მატერია არათანაბრადაა განაწილებული, მაგალითად გალაქტიკური ჯგუფები და გროვები) და არ იწვევს დრო-სივრცის სფერულად დეფორმირებას, წყარო (რომელიც ლინზირდება) დაემსგავსება ნაწილობრივ რკალებს, რომელიც ლინზის გარშემო არიან მიმოფანტულნი. დამკვირვებელმა შემდეგ შეიძლება დაინახოს იგივე წყარო მრავალფეროვნად დეფორმირებული. ამის რიცხვი და ფორმა დამოკიდებულია წყაროს, ლინზისა და დამკვირვებლის პოციზიებზე, და ასევე ლინზირებული ობიექტის ფორმაზე.
გრავიტაციული ლინზირების 3 ტიპი არსებობს:
1. ძლიერი ლინზირება: როდესაც ადვილად ჩანს დეფორმირებები, როგორიცაა "აინშტაინის რგოლების", რკალების და მრავალფეროვანი ხედების წარმოქმნა.
2. სუსტი ლინზირება: ეს ხდება, როდესაც უკან მყოფი წყაროების დეფორმირება არის ბევრჯერ მცირე და შეიძლება მოხდეს დეტექტირება წყაროების დიდი რაოდენობის ანალიზით, რადგან იპოვონ თანმიმდევრული დეფორმაციების მხოლოდ რამდენიმე პროცენტი. ეს ლინზირება სტატისტიკურად გამომჟღავნდება, როდესაც ფონური ობიექტების უმეტესი გაჭიმულობა შვეულადაა ლინზის ცენტრის მიმართულებით. დიდი რაოდენობის გალაქტიკების მიმართულებებისა და ფორმების გაზომვით, მათი მიმართულებები (საითკენაცაა მიმართული) შეიძლება იყოს საშუალო, რომ გაიზომის მალინზირებელი ველის მატრიცები ნებისმიერ რეგიონში. ეს შეიძლება გამოყენებული იყოს სივრცეში მასის გადანაწილების რეკონსტრუქციისთვის: უფრო ზუსტად, ბნელი მატერიის ფონური გადანაწილების რეკონსტრუქცია შეიძლება გაკეთდეს. რადგანაც გალაქტიკების უმეტესობა ელიფსურია და სუსტი გრავიტაციული ლინზირების სიგნალი ძალიან მცირეა, ამ დროს გალაქტიკათა ძალიან დიდი რაოდენობის უნდა იყოს გამოყენებული ამ დაკვირვებებში.
3. მიკროლინზირება: ასეთი ტიპის ლინზირების დროს არანაირი დეფორმირება არ შეიმჩნევა ფორმაში, მაგრამ უკან მყოფი ობიექტიდან წამოსული სინათლის რაოდენობა იცვლება დროთა განმავლობაში. ერთ ტიპურ შემთხვევაში ეს მალინზირებელი ობიექტი შეიძლება იყოს "ირმის ნახტომში" მყოფი ვარსკვლავები სხვა, შორეულ გალაქტიკაში არსებული ვარსკვლავების ფონით, ან, მეორე შემთხვევაში, უფრო შორეული კვაზარიც კი. მიკროლინზირებისას შეიძლება ლინზა ობიექტი შავი ხვრელიც იყოს. მიკროლინზირება იმიტომ ჰქვია, რომ ძირითადად ამ პროცესში მიკროობიექტები მონაწილეობენ (მაგ. შავი ხვრელი მიკროობიექტია)
ისტორია[რედაქტირება | წყაროს რედაქტირება]
აინშტაინის ფარდობითობის ზოგადი თეორიის თანახმად, მასა დრო-სივრცეს ზნექს, რათა წარმოქმნას გრავიტაციული ველები. აქედან გამომდინარე, დრო-სივრცე იწვევს სინათლის დამახინჯებას. ეს თეორია დადასტურდა 1919 წელს მზის დაბნელების დროს, როდესაც არტურ ედინგტონმა აღმოაჩინა, რომ ვარსკვლავებიდან წამოსული სინათლე, რომელიც ახლოს უვლიდა მზეს, იყო ოდნავ დეფორმირებული. მაშასადამე, ეს ვარსკვლავები პოზიცია შეცვლილები ჩანდნენ.
აინშტაინმა გააანალიზა, რომ ასევე ასტრონომიულ ობიექტებსაც შეეძლოთ სინათლის დამახინჯება და, მეტიც, სწორი მდომარეობებისას (ნაგულისხმევია სწორი განლაგება) ერთი წყაროს მრავალი სურათი წარმოიქმნებოდა. მას უწოდეს გრავიტაციული ლინზირება, ან ზოგჯერ გრავიტაციული მირაჟი.
გრავიტაციული ლინზების ძებნა[რედაქტირება | წყაროს რედაქტირება]
ადრე, გრავიტაციულ ლინზათა უმეტესობა შემთხვევითაა აღმოჩენილი. მათი ძებნა ჩრდილოეთ ნახევარსფეროში CLASS (Cosmic Lens All Sky Survey)-ის გამოყენებით 22 ახალი მალინზირებელი სისტემის აღმოჩენა მოხერხდა. ამან კი გახსნა მთლიანად ახალი გზა ძალიან შორეული ობიექტების აღმოჩენებისა, ხოლო ეს აღმოჩენები დაგვეხმარებიან კოსმოლოგიური პარამეტრების უკეთ გაგებაში. გამოდის, რომ მათი პოვნით სამყაროს უკეთ შევიცნობთ. იგივე კვლევა სამხრეთ ნახევარსფეროში იქნებოდა ძალიან კარგი ნაბიჯი ჩრდილოეთ ნახევარსფეროს შესავსებად. როგორც მოსალოდნელია, თუ ასეთი კვლევები დაიგეგმება კარგად პარამეტრიზირებული ინსტუმენტებითა და მონაცემებით, ჩვენ შეგვიძლია თავისუფლად ვივარაუდოთ, რომ ამ ყველაფერს ძალიან კარგი შედეგი ექნება.
რესურსები ინტერნეტში[რედაქტირება | წყაროს რედაქტირება]

- Video: Evalyn Gates – Einstein's Telescope: The Search for Dark Matter and Dark Energy in the Universe დაარქივებული 2018-09-02 საიტზე Wayback Machine. , presentation in Portland, Oregon, on April 19, 2009, from the author's recent book tour.
- Audio: Fraser Cain and Dr. Pamela Gay – Astronomy Cast: Gravitational Lensing, May 2007
