როტორი
ვექტორულ აღრიცხვაში როტორი არის ვექტორული ოპერატორი, რომელიც ახასიათებს სამგანზომილებიანი ვექტორული ველის ბრუნვით თვისებებს. სივრცის ნებისმიერ წერტილში როტორი წარმოადგენს ვექტორს, რომლის სიგრძე და მნიშვნელობა ახასიათებს ველის ბრუნვას ამ წერტილში.
გრადიენტისა და დივერგენციისგან განსხვავებით როტორი არ ექვემდებარება ცალსახა განზოგარებას უფრო მაღალი განზომილების სივრცეებისათვის.
განსაზღვრება[რედაქტირება | წყაროს რედაქტირება]
რაიმე F ვექტორული ველის როტორი, რომელიც აღინიშნება როგორც curl F ან ∇×F, რაიმე წერტილში განისაზღვრება ამ წერტილში განლაგებულ ვექტორებზე დაგეგმილების მეშვეობით. თუ არის ნებისმიერი ერთეულოვანი ვექტორი, F ველის როტორის პროექცია ვექტორზე განისაზღვრება როგორც ამ ვექტორის მართობულს სივრცეში აღებული წირითი ინტეგრალისა და ამ წირით შემოსაზღვრული არის ფართობის ფარდობის ზღვრული მნიშვნელობა, როდესაც ინტეგრების წირი მიისწრაფის წერილისკენ.

მათემატიკურად როტორის განმარტებას აქვს სახე
სადაც არის წირითი ინტეგრალი აღებული განსახილველი არის საზღვარზე, ხოლო |A| არის ამ არის ფართობი.
თუ (x1,x2,x3) არიან დეკარტის კოორდინატები და (u1,u2,u3) ქმნიან რაიმე სხვა კოორდინატთა სისტემას, მაშინ არის შესაბამისი ვექტორის სიგრძე. როტორის დანარჩენი კომპონენტების განტოლებები მიიღება ამ განტოლებიდან ინდექსების შემდეგი ციკლური გადანაცვლებით: 3,1,2 → 1,2,3 → 2,3,1.
გამოყენება[რედაქტირება | წყაროს რედაქტირება]
პრაქტიკაში ზევით მოყვანილი განმარტება იშვიათად გამოიყენება, რადგან როტორის გამოთვლა ხდება რომელიმე კონკრეტულ კოორდინატთა სისტემაში.
დეკარტის კოორდინატთა სისტემაში რაიმე F ველის (რომლის გეგმილებია [Fx, Fy, Fz]) როტორი ∇×F მოიცემა შემდეგი მატრიცის დეტერმინანტის მეშვეობით:
სადაც i, j, და k არიან ერთეულოვანი ვექტორები შესაბამისად x-, y-, და z-ღერძების გასწვრივ. ეს ფორმულა ასეც შეიძლება ჩიწეროს
ნებისმიერ კოორდინატთა სისტემაში როტორის რომელიმე გეგმილი მოიცემა როგორც
სადაც ε აღნიშნავს ლევი-ჩივიტას სიმბოლოს. ექვივალენტურ ვექტორულ განტოლებას აქვს სახე:
სადაც ek ერთეულოვანი ვექტორია შესაბამისი ღერძის გასწვრივ.
მაგალითები[რედაქტირება | წყაროს რედაქტირება]
მარტივი ვექტორული ველი[რედაქტირება | წყაროს რედაქტირება]
განვიხილოთ ვექტორული ველი, რომელიც წრფივად არის დამოკიდებული x და y კოორდინატებზე:
მისი გრაფიკი შემდეგნაირად გამოიყურება:

ვიზუალური დათვალიერებითაც ჩანს რომ ეს ველი ბრუნავს.
როტორის გამოთვლით მივიღებთ:
რომელიც უარყოფითია z მიმართულებით და მუდმივია სივრცეში, ანუ განსახილველი ველის 'ბრუნვის რაოდენობა' ერთნაირია სივრცის ნებისმიერ (x, y) წერტილში. შესაბამისად თავად როტორის გრაფიკს შემდეგი მარტივი ფორმა აქვს:
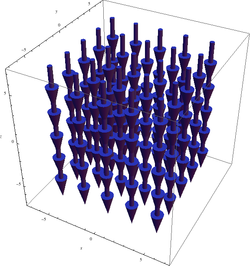
უფრო რთული მაგალითი[რედაქტირება | წყაროს რედაქტირება]
განვიხილოთ ვექტორული ველი:
რომლის გრაფიკს აქვს შემდეგი სახე:

ერთი შეხედვით ამ გრაფიკზე ბრუნვა არ ჩანს, მაგრამ თუ დავაკვირდებით ნახაზს ვნახავთ, რომ ველის მნიშვნელობა უფრო დიდია x=4 მნიშვნელობისთვის, ვიდრე x=3 მნიშვნელობისთვის. ინტუიციურად ცხადია, რომ თუ ამ არეში მცირე ბორბალისმაგვარ ნიჩაბს მოვათავსებთ, უფრო ძლიერი 'დინება' მარჯვნიდან გამოიწვევს ნიჩაბის ბრუნვას საათის ისრის მიმართულებით, რაც z ღერძის საპირისპირომ მიმართულ როტორს შეესაბამება.
როტორის გამოთვა გვაძლევს:
რომელიც ასევე გვიჩვენებს, რომ როტორი მიმართულია z ღერძის გასწვრივ უარყოფითი x-ებისთვის და z საწინააღმდეგოდ დადებით x-ებისთვის. ვინაიდან წინა მაგალითისგან განსხვავებით როტორი არ არის მუდმივი სივრცეში, მის გრაფიკს უფრო რთული სახე აქვს:
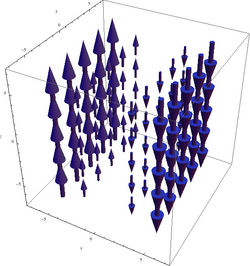
იგივობები[რედაქტირება | წყაროს რედაქტირება]
ნებისმიერი სკალარული ველის გრადიენტის როტორი იგივურად ნულის ტოლია:
თუ არის სკალარული ფუნქცია, ხოლო F არის ვექტორული ველი, მაშინ
იხილეთ აგრეთვე[რედაქტირება | წყაროს რედაქტირება]
სქოლიო[რედაქტირება | წყაროს რედაქტირება]
- Arfken, George B. and Hans J. Weber. Mathematical Methods For Physicists, Academic Press; 6 edition (June 21, 2005). ISBN 978-0-12-059876-2.
- Korn, Granino Arthur and Theresa M. Korn. Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review. New York: Dover Publications, გვ. 157–160. ISBN 0-486-41147-8.











![{\displaystyle {\nabla }\times \mathbf {F} =0{\boldsymbol {\hat {x}}}+0{\boldsymbol {\hat {y}}}+\left[{\frac {\partial }{\partial x}}(-x)-{\frac {\partial }{\partial y}}y\right]{\boldsymbol {\hat {z}}}=-2{\boldsymbol {\hat {z}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/28cd3fa48f892c1df357ac7060797eb7dd1a8572)




