სიმრავლე
ამ სტატიაში არ არის მითითებული სანდო და გადამოწმებადი წყარო. |
ამ სტატიას გრამატიკის, სტილისა და მართლწერის გასწორება სჭირდება. |
ამ სტატიას ან სექციას ვიკიფიცირება სჭირდება ქართული ვიკიპედიის ხარისხის სტანდარტების დასაკმაყოფილებლად. იმ შემთხვევაში, თუ არ იცით, თუ რა არის ვიკიფიცირება, იხ. დახმარების გვერდი. სასურველია ამის შესახებ აცნობოთ იმ მომხმარებლებსაც, რომელთაც მნიშვნელოვანი წვლილი მიუძღვით სტატიის შექმნაში. გამოიყენეთ: {{subst:ვიკიფიცირება/info|სიმრავლე}} |
სიმრავლე — ერთ-ერთი მნიშვნელოვანი ცნება მათემატიკაში. ის ზოგადად წარმოადგენს ნებისმიერ ობიექტთა ერთობლიობას. სიმრავლე შეიძლება იყოს ცარიელი (ცარიელი სიმრავლე). მასში ერთი და იმავე ობიქტის რამდენიმეჯერ განმეორებისას, ის აღიქმება ერთ ელემენტად. სიმრავლეთა თეორია არის მათემატიკის დარგი სიმრავლეებისა და სიმრავლეებზე ოპერაციების შესახებ.
სიმრავლეებს აღნიშნავენ დიდი ლათინური ასოებით. მაგალითად სიმრავლე, რომელიც შედგება ელემენტებისაგან, ჩაიწერება ასე .
სიმრავლე. ქვესიმრავლე[რედაქტირება | წყაროს რედაქტირება]
A = { a, b, c } და B = { a, b, c, x, y, z } A არის B ქვესიმრავლე, თუ ნებისმიერი ელემენტი მოიძებნება B სიმრავლეშიც.
- A = B, როცა და
ისტორიული ცნობა. სპეციალური სიმრავლეები[რედაქტირება | წყაროს რედაქტირება]
სანამ სპეციალურ სიმრავლეებს განვიხილავდეთ, მოკლედ მიმოვიხილოთ სიმრავლეთა თეორიის ჩამოყალიბების ისტორია. სიმრავლეთა თეორიის ფუძემდებლად ითვლება გერმანელი მათემატიკოსი გეორგ კანტორი (1845–1918). აი როგორ წარმოგვიდგენს ის სიმრავლეს: სიმრავლე არის ბევრი რომელსაც ჩვენ ერთ მთლიანობაში გავიაზრებთ. მის ქვეშ გვესმის ერთმანეთში შერწყმა ჩვენი მხედველობის ან აზრის გარკვეული ობიექტებისა რომლებიც ერთმანეთისაგან კარგად განირჩევიან. ბევრი მეცნიერი თვლიდა, რომ მათემატიკა სიმრავლეებზე დაფუძნებული მეცნიერებაა, სწორედ ამიტომ სიმრავლეებს მათემატიკის საფუძვლადაც მოიხსენიებდნენ. ერთ-ერთი პირველთაგანი იყო რიხარდ დედეკინდი, რომელიც შეეცადა სიმრავლის განმარტებას, როგორც ტომარისა, რომელშიც სხვადასხვა საგნებია მოთავსებული. ხოლო ცარიელი სიმრავლე წარმოადგინა როგორც ცარიელი ტომარა. დღეს საყოველთაოდაა მიღებული სიმრავლის მოცემის ერთ-ერთი ხერხი, რომელიც მათემატიკოს ჯონ ვენს უკავშირდება (ვენის დიაგრამა). სწორედ მან შემოიღო სიმრავლეთა ვენის დიაგრამებით მოცემა. ვენის დიაგრამებს იყენებდა ცნობილი მათემატიკოსი ლაიბნიციც. სასრული სიმრავლე შეიძლება მისი შემადგენელი ელემენტების ჩამოთვლით დაიწეროს, ხოლო უსასრულო სიმრავლე ამ სიმრავლის მახასიათებელი თვისების მიხედვით (ისეთი თვისებით, რომელიც მხოლოდ ამ სიმრავლის ელემენტებს გააჩნიათ). ახლა სპეციალურ სიმრავლეებზე ვისაუბროთ:
- ნატურალურ რიცხვთა სიმრავლეები და მისი ქვესიმრავლე .
- მთელ რიცხვთა სიმრავლე
- რაციონალ რიცხვთა სიმრავლე
- ნამდვილ რიცხვთა სიმრავლე (ასევე )
ახლა კი სიმრავლეებზე ალგებრულ ოპერაციებს განვიხილავთ.
ალგებრული ოპერაციები სიმრავლეებზე[რედაქტირება | წყაროს რედაქტირება]
სიმრავლეების ტოლობა[რედაქტირება | წყაროს რედაქტირება]
დავიწყოთ სიმრავლეთა ტოლობით::: ჩვეულებრივ ენაზე რომ ვთქვათ ეს ნიშნავს, რომ A სიმრავლის ყოველი ელემენტი ამავდროულად B სიმრავლის ელემენტიცაა, ხოლო B-ს ყველა ელემენტი A-ს ყველა ელემენტს შეესაბამება (ტოლია).
სიმრავლეების გაერთიანება[რედაქტირება | წყაროს რედაქტირება]
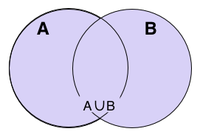
სიმრავლეთა გაერთიანება ნიშნავს ყველა იმ ელემენტის პოვნას, რომელიც ორივე სიმრავლეს ეკუთვნის (ანუ გაერთიანებულია ორი სიმრავლის ელემენტები) A-ს გაერთიანება B-სთან აღინიშნება, როგორც და ნიშნავს G := { x |სადაც ან }
მაგალითები:
სიმრავლეების თანაკვეთა[რედაქტირება | წყაროს რედაქტირება]
სიმრავლეთა თანაკვეთა გულისხმობს საერთო ელემენტების პოვნას ორ სიმრავლეს შორის. ორი სიმრავლის შემადგენლობაში შეიძლება იყოს ერთნაირი ელემენტები, სწორედ ასეთ ელემენტებს წარმოადგენს სიმრავლეთა თანაკვეთა. A-ს თანაკვეთა B-სთან ჩაიწერება შემდეგნაირად
სიმრავლეების სხვაობა[რედაქტირება | წყაროს რედაქტირება]
სიმრავლეების სხვაობა წარმოგვიდგენს ორი სიმრავლიდან მხოლოდ ერთს, თავისი შემადგენელი ელემენტებით, მიუხედავად ეკუთვნის თუ არა ის ამავდროულად მეორე სიმრავლეს. :::
სიმრავლის დამატება[რედაქტირება | წყაროს რედაქტირება]
B ⊆ A
ხშირად -ის ნაცვლად გამოიყენება ჩაწერის შემდეგი ხერხი .
























