დეკარტის კოორდინატთა სისტემა

დეკარტის კოორდინატების ილუსტრაცია სიბრტყეზე. ნაჩვენებია 4 წერტილი და მათი კოორდინატები: (2, 3) მწვანედ, (−3, 1) წითლად, (−1.5, −2.5) ლურჯად და კოორდინატთა სათავე (0, 0) შინდისფრად.

დეკარტის კოორდინატთა სისტემა განსაზღვრავს ნებისმიერი წერტილის მდებარეობას სიბრტყეზე ორი რიცხვის, კოორდინატების მეშვეობით, რომლებიც არიან დადებითი ან უარყოფითი რიცხვები, რომლებიც განსაზღვრავენ მანძილს ამ წერტილიდან ორ ფიქსირებულ ურთიერთმართობულ წრფეებამდე (კოორდინატთა ღერძებამდე).

კოორდინატთა ღერძებს ხშირაბ უბრალოდ ღერძებს უწოდებენ, ხოლო მათი გადაკვეთის წერტილს კი კოორდინატთა სათავეს.

ეს პრინციპი მარტივად შეიძლება განზოგადდეს სამგანზომილებიანი სივრცის შემთხვევაში. სამგანზომილებიან სივრცეში გვექნება სამი ურთიერთმართობული კოორდინატთა ღერძი, და რაიმე წერტილის მდებარეობა სივრცეში განისაზღვრება როგორც მანძილი ამ წერტილიდან კოორდინატთა ღერძების წყვილებზე გავლებულ სიბრტყეებამდე. ანალოგიურად, n განზომილებიან სირცეში წერტილის მდებარეობა შეიძლება დახასიათდეს n დეკარტის კოორდინატით.

დეკარტის კოორდინატთა სისტემა და მასზე მოცემული 2ის ტოლი რადიუსის წრეწირი (წითლად), რომლის ცენტრი კოორდინატთა სათავეშია. წრეწირის განტოლებას აქვს (x - a)² + (y - b)² = r² სადაც a და b არის წრეწირის ცენტრის კოორდინატები (a, b), ხოლო r არის მისი რადიუსი.

დეკარტის კოორდინატთა სისტემა შემოღებული იქნა რენე დეკარტის მიერ XVII საუკუნეში. ეს მოვლენა რევოლუციური იყო მათემატიკის ისტორიაში, რადგან პირველად გახდა შესაძლებელი ევკლიდეს გეემეტრიისა და ალგებრის სისტემური დაკავშირება. დეკარტის კოორდინატთა სისტემის გამოყენებით ნებისმიერი გეომეტრიული ფიგურის ფორმა შეიძლება ჩაწერილი იქნას დეკარტის განტოლებსის მეშვეობით, რომელიც წარმოადგენს ალგებრულ განტოლებას და აკავშირებს გეომეტრიული ფიგურის კოორდინატებს. მაგალითად, 2-ის ტოლი რადიუსის წრეწირი შეიძლება მოცემული იქნას როგორც ყველა იმ წერტილის ერთობლიობა, რომელთა კოორდინატები x და y აკმაყოფილებენ განტოლებასx² + y² = 4.

დეკარტის კოორდინატები წარმოადგენენ ანალიზური გეომეტრიის საფუძველს, და ინტენსიურად გამოიყენება მათემატიკის ბევრ სხვა დარგში, როგორიცაა წრფივი ალგებრა, კომპლექსური ცვლადის ფუნქციათა თეორია, დიფერენციალური გეომეტრია, ჯგუფთა თეორია და ა.შ. ისინი აგრეთვე ინტენსიურად გამოიყენება ასტრონომიაში, ფიზიკაში და სხვა მეცნიერებებში.

განმარტებები

რიცხვითი ღერძი

ერთგანზომილებინი სივრცეში, ანუ წრფეზე დეკარტის კოორდინატთა სისტემის განსაზღვრა გულისხმობს რაიმე O-წერტილის არჩევას (კოორდინატთა სათავე), სიგრძის ერთეულის არჩევას და ამ წრფეზე მიმართულების (ორიენტაციის) არჩევას. ეს უკანასკნელი გულისხმობს, რომ O-წერტილიდან გამომავალ ერთ ერთ სხივი (ნახევარწრფე) განისაზღვრება როგორც დადებითი, ხოლო მერე როგორც უარყოფითი. ამის შემდეგ იტყვიან, რომ ღერძის მიმართულება არის მიმართულება უარყოფითი ნახევრიდან დადებითი ნახევრისკენ. ასეთი არჩევის შემდეგ წრფეზე განლაგებული ყველა წერტილის შეიძლება დახასიათდეს O-სათავიდან ამ წერტილამდე მანძილით, რომელსაც მიენიჭება დადებითი ან უარყოფითი ნიშანი იმის მიხედვით თუ რომელ ნახევარწრფეზე არის განლაგებული წერტილი.

წრფეს მასზე განსაზღვრული დეკარტის კოორდინატთა სისტემით რიცხვითი ღერძი ეწოდება. ნებისმიერ რიცხვს იქნება ის ნატურალური, რაციონალური თუ ირაციონალური ასეთ წრფეზე ერთადერთი მდებარეობა შეესაბამება. და საპირისპიროდ, ნებისმიერი წერტილი წრფეზე შეიძლება დახასიათდეს ერთი რიცხვით.

დეკარტის კოორდინატები სიბრტყეზე

დეკარტის კოორდინატთა სისტემა ორ განზომილებაში (სიბრტყეზე) შედგება ორი პერპენდიკულარული წრფისგან (კოორდინატთა ღერძებისგან), ორივე ღერძისთვის განსაზღვრული ერთი და იმავე სიგრძის ერთეულისგან და თითოეული ღერძისთვის განსაზღვრული მიმართულებისგან. ამ ღერძებს ხშირად x და y-ღერძებს უწოდებენ, სადაც x-ღერძი როგორც წესი არის ჰორიზონტალური, ხოლო y-ღერძი ვერტიკალური. ღერძების გადაკვეთის წერტილი წარმოადგენს ათვლის წერტილს ორივე ღერძისთვის და შესაბამისად ორივე ღერძი წარმოადგენს ცალკე რიცხვით ღერძს.

ნებისმიერი P წერტილის კოორდინატები შემდეგნაირად განისაზღვრება. P წერტილიდან ავლებენ ორ ღერძს, პირველს, რომელიც x-ღერძის პერპენდიკულარულია და კვეთავს მას რაიმე X წერტილში, და მეორეს, რომელიც y-ღერძის პერპენდიკულარულია და კვეთავს მას Y წერტილში. P წერტილის x და y კოორდინატები სიბრტყეზე არის შესაბამისად X და Y.

დეკარტის კოორდინატები სამგანზომილებიან სივრცეში

სამგანზომილებიანი დეკარტის კოორდინატთა სისტემა, O კოორდინატთა სათავითა და X, Y, Z ღერძებით რომელთა ორიენტაცია ისრებით არის ნაჩვენები. დანაყოფები ღერძებზე შეესაბამება სიგრძის ერთეულებს. შავი წერტილი აღნიშნავს წერტილს კოორდინატებით X = 2, Y = 3, და Z = 4, ანუ (2,3,4).

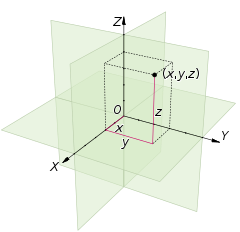
სიბრტყის ანალოგიურად ხდება დეკარტის კოორდინატების განსაზღვრა სამგანზომილენიან (N-განზომილებიან) სივრცეში, იმ განსხვავებით, რომ ამ შემთხვევაში არჩეული უნდა იქნას სამი (N) ურთერთმართობული წრფე და წერტილის მდებარეობა ამ სივრცეში შესაბამისად ხასიათდება სამი (N) კოორდინატით.

დეკარტის ფორმულები სიბრტყისთვის

მანძილი ორ წერტილს შორის

ევკლიდური მანძილი ორ წერტილს შორის, რომელთა დეკარტის კოორდინატებია $(x_{1},y_{1})$ და $(x_{2},y_{2})$ არის

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}.$

ეს განტოლება წარმოადგენს პითაგორას თეორემის დეკარტული სივრცის ვერსიას. სამგანზომილებიან სივრცეში მანძილი ორ წერტილს შორის, რომელთა კოორდინატებია $(x_{1},y_{1},z_{1})$ და $(x_{2},y_{2},z_{2})$ არის

$d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}+(z_{2}-z_{1})^{2}}}$

ეს ტოლობა შეიძლება მიღებული იქნას პითაგორას თეორემის ორჯერადი გამოყენებით.

ევკლიდური გარდაქმნები

წანაცვლება

წერტილების რაიმე ერთობლიობის წანაცვლება სიბრტყეზე მათ შორის მანძილების შეუცვლელად ექვივალენტურია ყველა ამ წერტილის დეკარტის კოორდინატებისთვის რიცხვების ფიქსირებული წყვილის (X,Y) მიმატებისა. ანუ, თუ წანაცვლებამდე რაიმე წერტილის კოორდინატები იყო (x,y), წანაცვლების შემდეგ გვექნება

$(x',y')=(x+X,y+Y).\,$

მასშტაბური ინვარიანტობა

რაიმე წერტილების ერთობლიობისგან შედგენილი ფიგურის ზომის გაზრდა ან შემცირება ექნივალენტურია ამ ფიგურის ყველა წერტილის დეკარტის კოორდინატების ერთიდაიმავე დადებით m რიცხვზე გამრავლებისა. თუ (x,y) არის საწტისი ფიგურის რაიმე წერტილის კოორდინატები, მაშინ მასშტაბშეცვლილი ფიგურის შესაბამისი წერტილის კოორდინატი იქნება

$(x',y')=(mx,my).\,$

თუ m 1-ზე მეტია, მაშინ ფიგურის ზომა იზრდება, ხოლო თუ m-ის მნიშვნელობა 0-სა და 1-ს შორიასაა, მაშინ მცირდება.

ბრუნვა

კოორდინატთა სათავის მიმართ რაიმე ფიგურის საათის ისრის საწინააღმდეგო მიმართულებით რაიმე $\theta$ კუთხით მობრუნება ექვივალენტურია საწყისი ფიგურის ყველა წერტილის (x,y) დეკარტის კოორდინატების ახალი კოორდინატებით (x',y') შეცვლით, სადაც

$x'=x\cos \theta -y\sin \theta \,$

$y'=x\sin \theta +y\cos \theta .\,$

ანუ, ექვივალენტურად $(x',y')=((x\cos \theta -y\sin \theta \,),(x\sin \theta +y\cos \theta \,)).$

არეკვლა

თუ (x, y) სიბრტყეზე რაიმე წერეტილის დეკარტის კოორდინატებია, მაშინ (−x, y) არის მეორე (Y) ღერძის მიმართ მისი არეკვლის შედეგად მიღებული წერტილის კოორდინატები, ხოლო (x, −y) არის X-ღერძის მიმართ არეკვლის შედეგად მიღებული წერტილის კოორდინატები.

ზოგადი გარდაქმნები

სიბრტყეზე ევკლიდური გარდაქმნებია წანაცვლება, მასშტაბის შეცვლა, ბრუნვა არეკვლა და მათი რამე კომბინაცია. რაიმე $(x,y)$ წერტილის ნებისმიერი ევკლიდური გარდაქმნის შედეგი $(x',y')$ მოიცემა შემდეგი ფორმულით

$(x',y')=(x,y)A+b\,$

სადაც A არის 2×2 მატრიცა ხოლო b არის რაიმე რიცხვების წყვილი, რომელიც დამოკიდებულია განხორციელებულ გარდაქმნაზე. გაშლილი ფორმით ეს განტოლება შემდეგნაირად ჩაიწერება

$x'=xA_{11}+yA_{21}+b_{1}\,$

$y'=xA_{12}+yA_{22}+b_{2}.\,$

A მატრიცას უნდა ჰქონდეს ორთოგონალური მწკრივები ერთი და იმავე ევკლიდური სიგრძით, ანუ უნდა სრულდებოდეს პირობები

$A_{11}A_{21}+A_{12}A_{22}=0\,$

და

$A_{11}^{2}+A_{12}^{2}=A_{21}^{2}+A_{22}^{2}.$

ამ ორი განტოლების დაკმაყოფილება ექვივალენტურია პირობისა, რომ A მატრიცის ნამრავლი მის ტრანსპონირებულ მატრიცაზე არის დიაგონალური მატრიცა. თუ A მატრიცა ამ პირობებს არ აკმაყოფილებს, მაშინ საქმე გვაქვს უფრო ზოგად, აფინურ გარდაქმნებთან.

ზემოთ მოყვანილი ფორმულა შეესაბამება წანაცვლებას მხოლოდ მაშინ, როდესაც A არის ერთეულოვანი მარტიცა.

ვექტორის წარმოდგენა სტანდარტულ ბაზისში

რაიმე წერტილი დეკარტის კორდინატთა სისტემაში შეიძლება წარმოდგენილი იქნას აგრეთვე როგორც ვექტორი, რომლის ერთი ბოლო მდებარეობს კოორდინატთა სათავაში, მეორე ბოლო განსახილველ წერტილში და მიმართულია სათავიდან წერტილისკენ. ასეთი ვექტორი რომელსაც ხშირად რადიუს-ვექოტს უწოდებენ ხშირად აღნიშნავენ როგორც $\mathbf {r}$. სამგანზომილებიან სივრცეში კოორდინატთა სათავიდან რაიმე $(x,y,z)$ დეკარტის კოორდინატების მქონე წერტილში მიმართული ვექტორი ჩაიწერება როგორც:

$\mathbf {r} =x\mathbf {i} +y\mathbf {j} +z\mathbf {k}$

სადაც $\mathbf {i}$, $\mathbf {j}$, და $\mathbf {k}$ არიან ერთეულოვანი ვექტორები შესაბამისად $x$, $y$, და $z$ ღერძების გასწვრივ.

იხილეთ აგრეთვე

• ცილინდრულ კოორდინატთა სისტემა.
• სფერულ კოორდინატთა სისტემა.
• გრადიენტი.
• დივერგენცია.
• როტორი.
• ვექტორული აღრიცხავა.